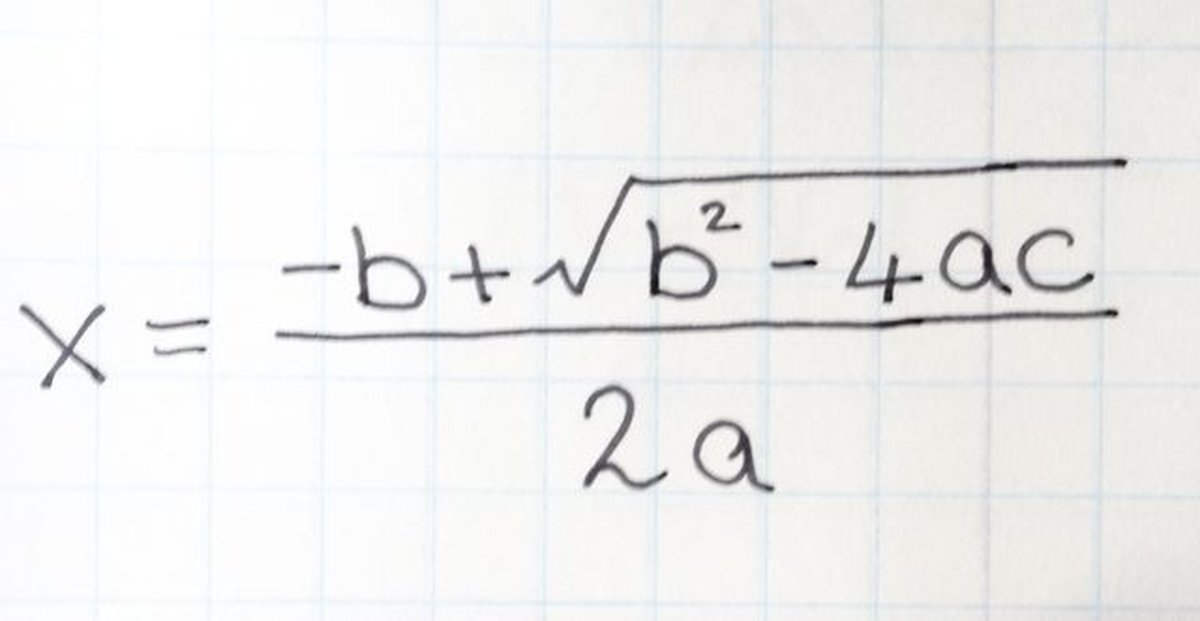Can see how this gives a proof of the root formula that is less cryptic for students.

Now I was wondering naively whether this trick could be used to quickly find one root of higher degrees polynomials.
Like x3 +b x2 + c x +d, where the sum of the roots is -b and their product is -d.
So I write x1 = -b/3 + u1, x2 = -b/3 + u2, x3 = -b/3 - u1 -u2.
But solving for u2(u1) starting for the product is quite barbaric.
Maybe there’s a better organisation of the u variables?

I like this approach. It seems conceptually easy enough for my middle school students to understand. Now to try it out with them…

With the thumbnail I expected a simpler expression of the quadratic formula, which is already very easy to use. His method also doesn’t work for equations where the aX² term doesn’t have a=1.