So I found out about Marx’ mathematical manuscripts, so I say “Hey, I’ve been studying mathematics this year at university. I understand limits and derivatives, maybe I can understand something of that gibberish.” So I see the titles and the one called “On the Concept of the Derived Function”, I go there and I see some notation I don’t understand, he speaks about things I’m not clearly understanding, so maybe some of you could make it clear.
For example:
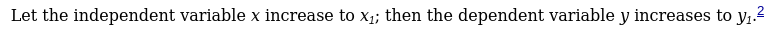
Why is this x sub 1 notation? Is this some other way to write derivatives? Because on the footnotes it says this:
- In order to avoid confusion with the designation of derivatives, Marx’s notation x´, y´, … for the new values of the variable has been replaced here and in all similar cases by x1, y1, …
Then I saw a talk about Marx’s mathematics and the infinitesimal and some of that stuff, but the one who was speaking didn’t went much into the mathematical part but was more like a history talk on how the Chinese were interested in the propositions of Marx because it liberated calculus from the idealist veil with which it was conceived by Leibniz and Newton, but the one who was talking mentioned Marx learning mathematics with whatever he had around and didn’t managed to read Cauchy so we was like “Yeah this is nice but it’s al shit now we have proved it fully works.” But well, he seems a bit biased, since he’s a Usonian, so maybe Marx’s writings are still relevant, I don’t even know who the fuck Cauchy is, so yeah, help.
Text: https://www.marxists.org/archive/marx/works/1881/mathematical-manuscripts/ch03.html
I’d love to read a breakdown thread of this text if u ever fully detangle it. Maybe u could apply the same critical logic to Cauchy that Marx applies to earlier theorists.
I feel like the “standard model” of any field of science on some level betrays the often limiting assumptions foundational to that field, which makes a historical materialist approach to mathematics very intriguing. How to model change, whether mathematically or socially, is a very philosophical question.
Well, really, really, really rough tl;dr, but basically Marx writings still hold up in some way, Cauchy formalized Leibniz/Newton theory, derivatives are still a somewhat shady mathematical subject which nevertheless provides good results in praxis.
Marx’s economic and political writings are still relevant, I’m sure his mathematics are on point too. I’m not a mathematician and to be honest you’re the first Marxist I’ve seen who is. So with that I say I can’t help you but thank you for existing, please maintain and further develop because math is very beneficial 👍


