Kind of intentionally obtuse since they used eₑ as a variable and eₑₑ as another variable, and used (e-e) as an exponent a few times, which is basically the equivalent of multiplying by 1 in a fancy way. The first and last term also perfectly cancel out.
The same integral written in a saner form is:
integral from -e^e to e^e of (integral from -e^e to e^e of e^-(x^2+y^2)dy)dx
Wait… that’s not an approximation at all! That equals exactly pi. If I understand the math correctly, it’s effectively a formula for the area of a unit circle.
That should be an approximation. To get exactly pi the range of both integrals should be from minus infinity to infinity like this. It’s the integral of the 2D Gaussian, which is fairly known.
The approximation is only around 4.28*10^-101 off from pi.
https://www.wolframalpha.com/input?i=integral+from+-a+to+a+of+(integral+from+-a+to+a+of+e^-(x^2%2By^2)dy)dx
https://www.wolframalpha.com/input?i=(1-erf(e^e)^2)*piAnd because it always bears repeating;
According to JPL’s Chief Engineer for Mission Operations and Science, Marc Rayman-
Let's go to the largest size there is: the known universe. The radius of the universe is about 46 billion light years. Now let me ask (and answer!) a different question: How many digits of pi would we need to calculate the circumference of a circle with a radius of 46 billion light years to an accuracy equal to the diameter of a hydrogen atom, the simplest atom? It turns out that 37 decimal places (38 digits, including the number 3 to the left of the decimal point) would be quite sufficient.So the number 3 should be close enough for home use. Good to know. Thanks!
As an engineer, I approve this message!
My maths exam asked me to consider pi=5.
“I will… consider it.”
You can quote with the “greater than” sign (>). Backticks mark text as source code.
> quote
Ah, you’re right. I was thrown off by WolframAlpha saying the integral = π ≈ 3.1416 Both of those should be ≈
(x^2 + y^2)=1 is the equation for a unit circle, so it’s definitely related. Just not quite how I thought.
Also the 2D gaussian integral is used to give an insight on why the 1D gaussian integral is sqrt of pi. Here is a video with cool visualization for anyone interested.
“Fix” it with
Lim as eee-> infinity(where eee is some other e-named variable)
When did dolphins learn calculus?

it ends in deeedee so maybe this is dexter when his sister has used the mosquito-izer on him and he’s angrily yelling at her
And then he murders her while maintaining his secret identity as a forensic technician?
This is a fantastic metaphor for what tinnitus feels like.
e
For some reason in my head, “eeeeeeeeeeeee de eee de e” is the sounds a toddler makes when you take them to a play ground and they just start to run in wide arcs - unable to decide which piece of equipment to play on first.
So, of course, the integral of “eeeeeeeeeeeee de eee de e” would be the sound of them sleeping the car on the way home.
You may just have made me create pattern screamer and I don’t exactly think it’s happy at you.
Is nobody going to complain this is a screenshot of a Tumblr post of a Reddit post
I can’t even upvote this; it’s too hideous.
That’s why I upvoted it.
I love it but I do not understand
“e”, or Euler’s number, is a constant used in maths because it has useful properties in logarithms and some other things. Basically just like pi except for logarithms instead of circles. Like pi, it’s an infinitely long series of non-repeating digits. The crime you have witnessed in the post is a shitload of mathematical operations applying e to e in various ways in order to get (very close to) pi. Like saying “I’m going to make 14 using only 2” and then saying (222)-2, except instead of 2 and 14 you’ve got e and pi
Formatting messed up (on my client at least.) It’s
2^2^2, but it looks like(2^2)2(without the parentheses, of course.)That was the intention, yes. Thanks
So it is not really approximating pi and there is no circle hiding?
It’s approximating the value of the actual number pi, 3.14159 etc. It’s not doing anything with pi after that
Donno if it’s part of the joke but there is a beautiful equation:
eiπ+1=0
So once you allow yourself to use i and log and stuff, you get a nice and simple equation
They’re also doing some shenanigans with the variable of integration. I bet it would look a lot more palatable if they were changed
But what does it sound like as musical notes?
That is actually really nice sounding
Wow nice work
Pretty monotonous. It’s just E.
I’m imagining fax sounds
Alan Becker should’ve used this
Not an equation though.
But it equals 3.14159265359
What is it?
Could be the right hand side or the left hand side of an equation* or of an inequation** whatever.
(*) equations have “=” in middle
(**) inequations have “=<” (or …) in middle.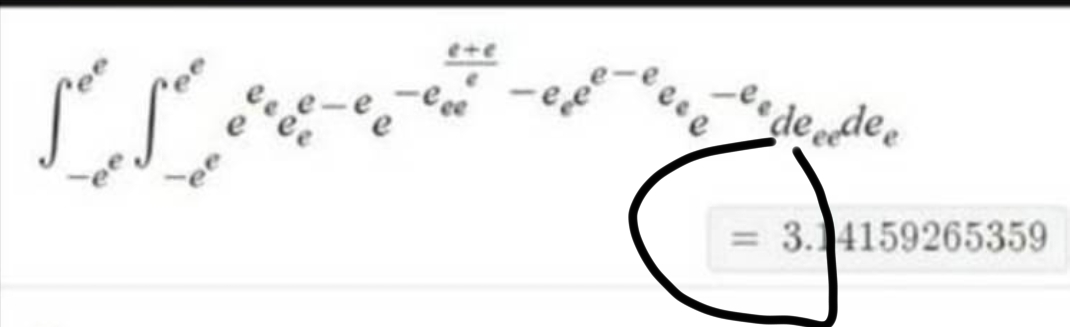
How the fuck did I miss that?
I’ve never seen one before - no one has - but I believe it’s a white hole.
deleted by creator
Psst, remove the space between ] and (