Understanding the nature of consciousness is one of the hardest problems in science. Some scientists have suggested that quantum mechanics, and in particular quantum entanglement, is the key to unraveling the phenomenon.
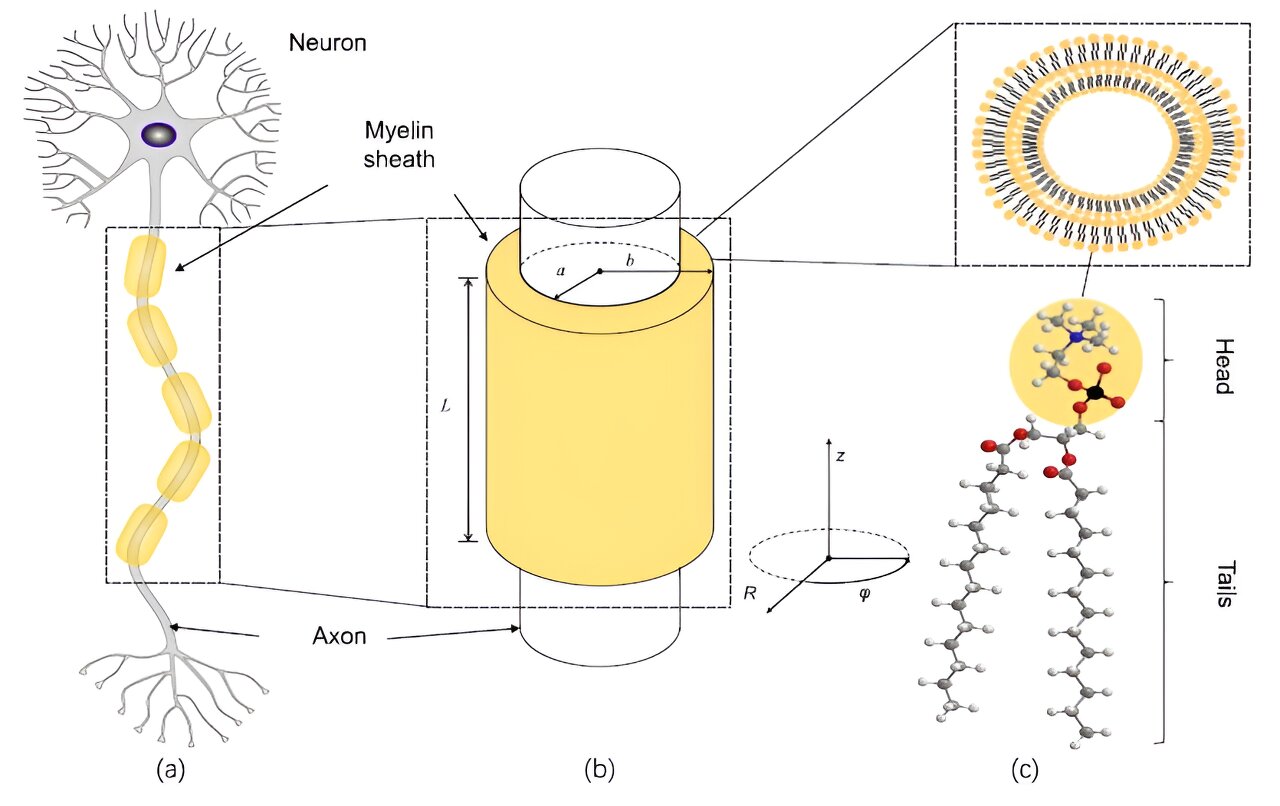
The brain communicates within itself by firing electrical signals called synapses between neurons, which are the main components of nervous tissue. It is the synchronized activity of millions of neurons that consciousness (among other brain business) relies on. But the way this precise synchronization takes place is unknown.
Entanglement means the two-photon state is not a classical combination of two photon states. Instead, measuring or interacting with one of the photons instantly affects the same property of the second photon, no matter how far away it is.
Entanglement has been demonstrated for a system whose members are over 1,000 km apart. Nothing like it exists in classical physics; it is purely a quantum phenomenon. Here entanglement would raise the possibility of much faster signaling along the sections of myelin that encase segments of the axon’s length.
One possibility, the authors write, is that the entanglement of photons could transform into entanglement along potassium ion channels in the neuron. If so, the opening and closing of one channel may affect the performance of another somewhere else.


The argument for this has never been convincing. People like Roger Penrose have argued that because people can believe things without proof, therefore consciousness is “special” in the sense that it can do something uncomputable, so it must not be reducible to classical physics. This argument is just bizarre, humans believe things without proof because they they don’t operate on proof but on confidence levels. They believe things that seem right to them based on their past experiences. Even AI operates on confidence levels and can say things that are false.
I have never seen a convincing argument that there really is something unique about human cognition that requires introducing anything quantum or even anything supernatural as it is popular for many philosophers in academia to argue these days.
This is just patently false. Entanglement is just a statistical correlation but one over quantum probabilities rather than classical probabilities (these can be distinguished by doing a trace over a density matrix). If you have two entangled particles, let’s say they are two electrons with a 50% chance of both being spin up or down, so the only possibilities are ⇑⇑ or ⇓⇓ with no other possibilities. That means they are statistically correlated as measuring one tells you the value of the other.
Now, let’s say, while they are still entangled, you flip the second one. If it’s supposedly true that altering one would instantly affect the other, then this should not alter the outcome. If the first was going to be ⇑ and the second was going to be ⇑, and you flip the second prior to measuring it, then it would affect the first one so they would both become ⇓⇓.
Yet, this is not what happens in practice. In practice, if you flip the second one prior to measuring it, you find the statistical correlation changes to two possibilities of ⇑⇓ and ⇓⇑. This is exactly what you would even expect classically. If I give you two envelopes where inside of them there is a card facing up and the other there is a card facing down, and I guarantee that they are random but correlated such that both envelopes have the card facing the same direction, if you flip over one of the cards before opening it, then you would expect then to then be the opposite directions rather than the same.
There is no actual evidence measuring a particle in an entangled pair affects the other particle. These affects only exist if you make certain metaphysical assumptions that go beyond quantum mechanics. If you presume objective collapse or hidden variables, for example, then you have to posit such affects. But traditional quantum mechanics is not an objective collapse theory or a hidden variable theory.
No. There is literally theorem called the No-signaling Theorem in quantum mechanics which proves such a thing is impossible.