Abstract
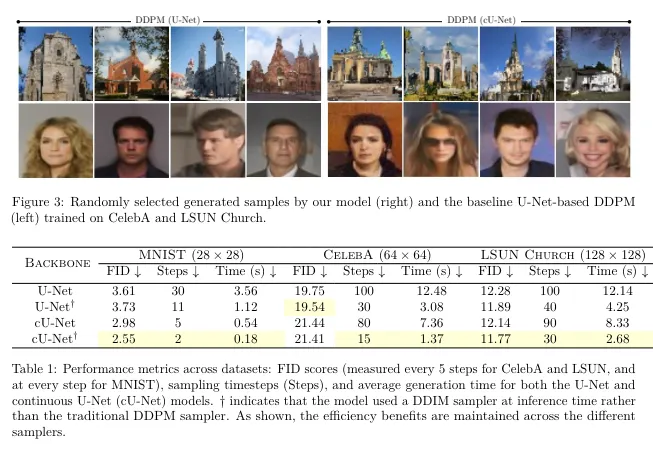
Diffusion Probabilistic Models stand as a critical tool in generative modelling, enabling the generation of complex data distributions. This family of generative models yields record-breaking performance in tasks such as image synthesis, video generation, and molecule design. Despite their capabilities, their efficiency, especially in the reverse process, remains a challenge due to slow convergence rates and high computational costs. In this paper, we introduce an approach that leverages continuous dynamical systems to design a novel denoising network for diffusion models that is more parameter-efficient, exhibits faster convergence, and demonstrates increased noise robustness. Experimenting with Denoising Diffusion Probabilistic Models (DDPMs), our framework operates with approximately a quarter of the parameters, and ∼ 30% of the Floating Point Operations (FLOPs) compared to standard U-Nets in DDPMs. Furthermore, our model is notably faster in inference than the baseline when measured in fair and equal conditions. We also provide a mathematical intuition as to why our proposed reverse process is faster as well as a mathematical discussion of the empirical tradeoffs in the denoising downstream task. Finally, we argue that our method is compatible with existing performance enhancement techniques, enabling further improvements in efficiency, quality, and speed.
Paper: https://arxiv.org/abs/2310.20092
Didn’t Lightning from ByteDance already do this?


