5
Symmetric tangled Platonic polyhedra
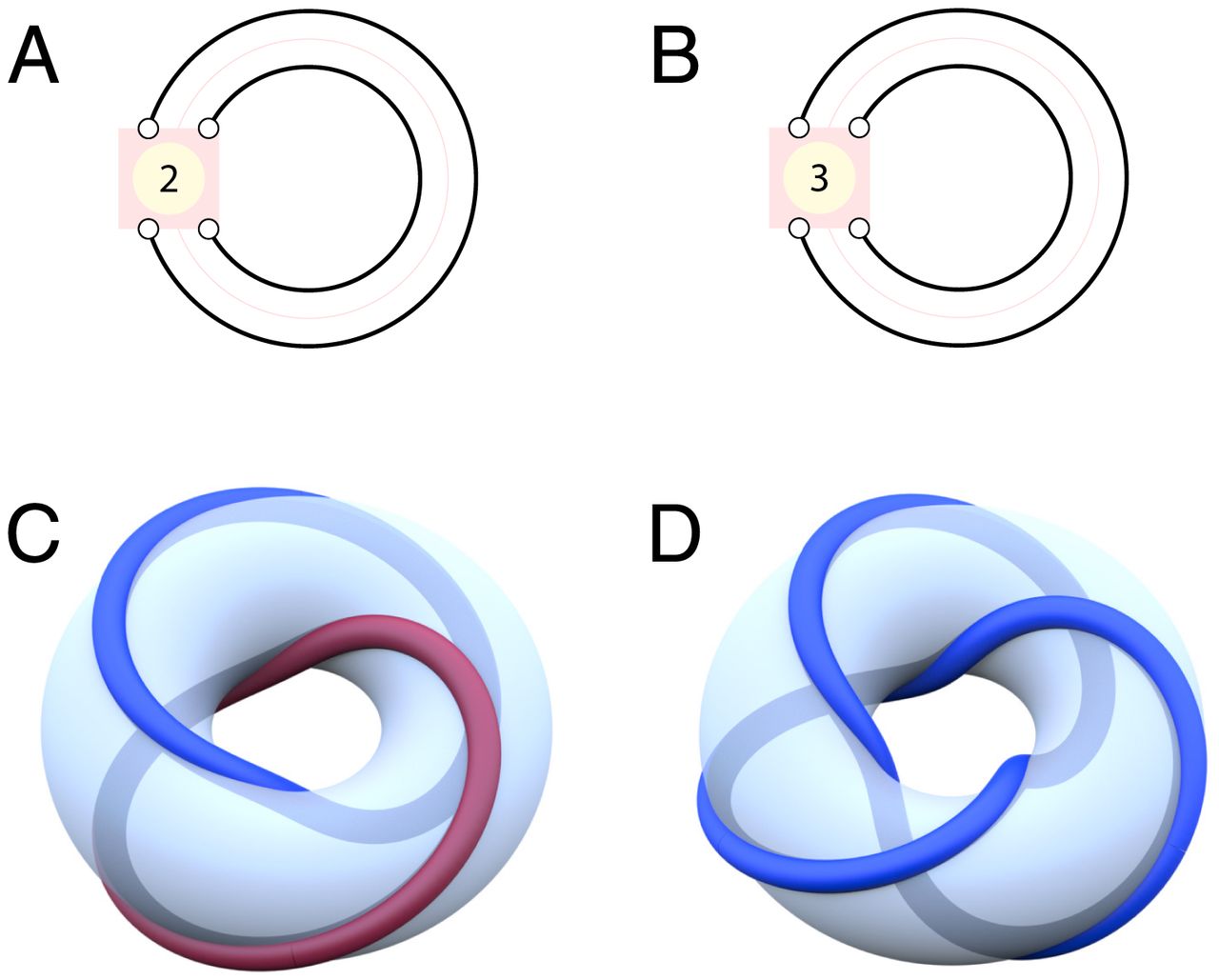
www.pnas.orgTangled tetrahedra, octahedra, cubes, icosahedra, and dodecahedra are generalizations of classical—untangled—Platonic polyhedra. Like the Platonic polyhedra, all vertices, edges, and faces are symmetrically equivalent. However, the edges of tangled polyhedra are curvilinear, or kinked, to allow entanglement, much like warps and wefts in woven fabrics. We construct the most symmetric entanglements of these polyhedra via assemblies of multistrand helices wound around edges of the conventional polyhedra; they are all necessarily chiral. The construction gives self-entangled chiral polyhedra and compound polyhedra containing catenated multiple tetrahedra or “generalized θ -polyhedra.” An unlimited variety of tangling is possible for any given topology. Related structures have been observed in synthetic materials and clathrin assemblies within cells.
Data files (in.ply format) allowing three-dimensional viewing of some of the tangled polyhedra discussed in this paper, plus a table listing components numbers, have been deposited in GitHub (). All other study data are included in the article and/or [ SI Appendix ][1].
[1]: https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2110345118/-/DCSupplemental


It’s always the torus that brings everything together.